통계적 학습

📌 통계적 학습 (Statistical learning)

 통계적 학습은 통계와 함수적 분석으로부터 그려진 머신러닝을 위한 뼈대로서,

데이터에 기반을 둔 예측 가능한 함수를 찾는 문제를 다룹니다.

 

본격적인 내용에 앞서 변수와 f 추정에 대한 기본적인 내용입니다.

X는 예측변수, 독립변수, 변수(predictors, independent variables, variables) 등의 이름으로 불리고,

Y는 반응변수, 종속변수(response or dependent variable) 등으로 불립니다.

X : n×p matrix, xij : the value of the jth variable for the ith observation

우리는 반응변수 Y 와 p개의 예측변수, X1, X2, … , Xp를 관찰합니다.

그리고 $ Y $ 와 $X=(X_1,X_2,...,X_p)$  둘 사이에 관계가 있다고 가정하고 아래의 형태로 그 관계를 표현합니다.

$$ Y=f(x)+\epsilon $$

 

f : some fixed, unknown function of X,

ε : a random error term, independent X , 평균이 0

 

👉 목표 : f 추정하기

우리는 아래의 식을 사용하여 f를 추정합니다.

$$ \hat{Y}=\hat{f}(X) $$

 

우리가 추정한 f, Y 등은 f hat, Y hat로 표시하고 이는 실제 f, Y와 구분하기 위한 것입니다.

 

왜 f를 추정할까?

① prediction(예측) ② inference(추론)

📌 모수적 방법 vs 비모수적 방법

How do we estimate f?

모수적 방법(Parametric metods)

• 먼저 X와 Y의 관계에 대해 가정을 한 뒤 f를 추정한 뒤 다시 가정한 것과 비교하는 방법입니다.
• 가정의 parameter 일부만 예측하는 것으로 문제가 축소되고 다양한 분석과 예측이 가능합니다.
• 만약 선택된 모델이 실제 f와 거리가 멀다면 추정이 잘못된 것이며, 가정이 틀리면 분석 자체가 의미가 없어집니다.

→ Linear regression, logistic regression, linear SVM, LDA, QDA 등

비모수적 방법(Non-parametric methods)

• X와 Y의 관계에 대한 명확한 가정 없이 가능한 한 데이터 포인트들과 가까운 점들을 얻어 f를 추정합니다. 가정이 없는 추정 방법이라 가정이 틀릴 위험이 없습니다.
• 정확한 추정을 위해 매우 많은 관찰(observations)이 필요합니다.
• 다양한 분석을 할 수 없습니다.

→ thin-plate spline, KNN, kernel SVM, decision tree 등

📌 지도 학습 vs 비지도 학습

지도 학습(Supervised learning)

• 반응변수 Y가 존재하는 학습입니다. 당연히 예측변수 X도 존재합니다.

	회귀문제(regression problem)	분류문제(classification problem)
Y	quantitative한 값.	유한하고 비정렬한 값.
e.g.	가격, 혈압 등	생존/사망, 자릿수 0-9, cancer class of tissue sample

비지도 학습(Unsupervised learning)

• 반응 변수 Y가 없고 예측 변수로만 샘플을 분석해야하는 학습입니다.
• Objective is more fuzzy – find groups of samples that behave similarly, find features that behave similarly, find linear combinations of features with the most variation.
• 내가 수행한 것이 얼마나 잘 된 것인지 알기 어렵습니다.

📌 훈련, 테스트, 검증 세트

훈련 세트(Training set)

• 학습에 사용되는 예시의 데이터 셋, 즉 주어진 데이터로 파라미터들에 적합합니다.
• 경험적 관계에 대해 훈련 세트를 검색하는 대부분의 접근 방식은 데이터에 과대적합되는 경향이 있어서 일반적으로 유지되지 않는 훈련 세트의 명백한 관계를 식별할 수 있다.

※ 과대적합(overfit) : training MSE는 작은데 test MSE는 커지는 상황

테스트 세트(Test set)

• 훈련 세트와 독립적이지만 같은 확률분포(probability distribution)을 따르는 데이터 셋이다.
• 모델을 수행하여 주어질 데이터

검증 세트(Validation set)

• 분류기(classifier)의 하이퍼 파라미터를 조정하는데 사용되는 예제 세트이다.

📌 모델의 정확도 평가

• 주어진 데이터에 대해 어떤 방법이 최상의 결과를 산출하는지 결정하는 것은 중요한 업무입니다.

---

For quantitative y,

 

$$Training\;MSE=\frac{1}{n}\sum _{i=1}^n(y_i-\hat{f}(x_i))^2,for\;training\;data\;(x_i,y_i)$$

$$ Test\ MSE=\frac{1}{n}\sum _{i=1}^n(y_{0i}-\hat{f}(x_{0i}))^2,\ for\ test\ data\ (x_{0i}\ ,\ y_{0i}) $$

 

가장 낮은 training MSE라고 해서 가장 낮은 test MSE를 제공하는 것은 아니며 심지어 다른 모델보다 성능이 더 안 좋을 수 있습니다.

가장 낮은 training MSE가 아니라 가장 낮은 test MSE를 제공하는 방법을 선택해야 합니다.

실전에서 training MSE는 비교적 계산하기 쉽지만, test MSE는 사용 가능한 테스트 데이터가 없기 때문에 계산하기 어렵습니다.

→ cross validation

---

$$ Expected\ test\ MSE\ :\ E(y_0-\hat{f}(x_0))^2=Var(\hat{f}(x_0))+[Bias(\hat{f}(x_0))]^2+Var(\epsilon) $$

• Flexibility
  • 우리가 가진 데이터에 얼마나 유연하게 fit하여 f를 추정하는지 의미한다. 즉, 얼마나 단순화를 최소화한 모델인지를 나타낸다.
  • flexibility↓ : 단순한 모델, flexibility↑ : 복잡한 모델
  • flexible 할수록 해석력을 잃기 때문에 적절한 조정이 필요하다.
• 분산(Variance)
  • 다른 training set를 사용하여 추정한 경우 변화하는 양이다. 즉 데이터에 얼마나 의존적인가를 나타낸다.
  • 더 flexible한 통계 방법은 variance가 더 높다.
• Bias(잔차가 아님)
  • 실생활 문제를 approximating할 때 발생하는 오류이다. 즉 를 나타낸다.
  • 예상하는 결과가 얼마나 맞는지
  • 더 flexible한 통계방법은 bias가 더 낮다. 
  •  

      $Bias\left(\hat{f}\left(x\right)\right)=E\left(\hat{f}\left(x\right)-f\left(x\right)\right)=E\left(\hat{f}\left(x\right)\right)-f\left(x\right)$

 

통계적 학습 방법의 좋은 테스트 세트는 낮은 squared bias뿐만 아니라 낮은 variance를 요구합니다. (Expeted test MSE 식 참고)

하지만 아주 작은 squared bias나 아주 작은 variance는 동시에 일어나기 힘든 경우이므로 두 값이 모두 작을 경우 모델을 의심해 볼 필요가 있습니다.

모델의 flexibility에 따라 bias와 variance는 반비례와 비슷한 변화를 보이는데,이는 필연적으로 bias variance trade-off 관계라는 것입니다.

bias가 매우 낮지만 variance는 높은 방법에는 모든 single training observation을 통과하는 곡선을 그리기 등, variance가 매우 낮지만 bias가 높은 방법에는 데이터에 수평선을 맞추기 등이 있는데,

bias나 variance 둘 중 하나가 완전히 작으면 나머지 하나가 커지므로 둘의 균형을 고려하여 적절한 값을 찾아야 합니다.

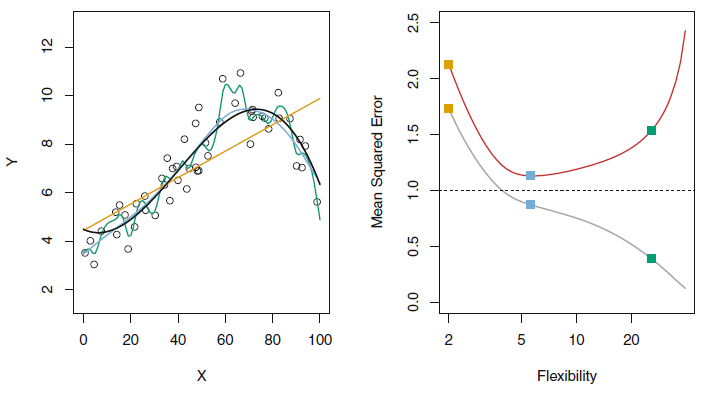
=> flexibility ↑, variance ↑, squared bias ↓, test MSE U, training MSE ↓